FUVEST - Física - calorimetria
(2007) Dois recipientes iguais A e B, contendo dois líquidos diferentes, inicialmente a 20°C, são colocados sobre uma placa térmica, da qual recebem aproximadamente a mesma quantidade de calor. Com isso, o líquido em A atinge 40°C, enquanto o líquido em B, 80°C. Se os recipientes forem retirados da placa e seus líquidos misturados, a temperatura final da mistura ficará em torno de
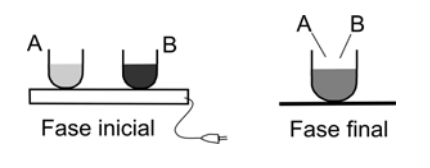
a) 45°C b) 50°C c) 55°C d) 60°C e) 65°C
Resolução:
-Análise inicial do problema:
Ambos líquidos recebem a mesma quantidade de calor e a temperatura do líquido B sobe mais que a do líquido A. Quer dizer que líquido A precisa de mais calor para subir sua temperatura, do que o líquido B . Em outras palavras, o calor específico (c) do líquido A é maior do que o do líquido B.
Depois, a fonte de calor é retirada, e os líquidos são misturados. Qual a temperatura final? Entendo que seria uma tentação escolher a temperatura intermediária entre 40 ºC e 80 ºC, que seria 60 ºC. Esta certamente seria a resposta se os líquidos fossem iguais . Mas já sabemos, após nossa análise inicial do problema, que o A possui maior calor específico.
Antes de iniciarmos os cálculos, podemos já eliminar algumas alternativas. Estando os 2 líquidos misturados, sem fonte de calor externa (placa quente), calor do líquido mais quente será transferido para o mais frio. Como c é mais alto para o líquido A, a temperatura final da mistura será menor que 60 ºC.
-Cálculos - (revisar teoria)
-Parte 1
Ambos líquidos recebem a mesma quantidade de calor então QA= QB, sendo:
QA = cA mA ΔT = cA mA (40-20) = cA mA*20
QB = cB mB ΔT = cB mB (80-20) = cB mB*60
Acima apenas colocamos os números nas fórmulas. Agora igualamos as duas:
cA mA*20 = cB mB*60 ==> cA mA = 3 cB mB (I)
-Parte 2
Quando se mistura um líquido a 40 ºC e outro a 80ºC , a temperatura final (Tf ) será intermediária. Ou seja, o calor fluirá do líquido mais quente para o mais frio. Podemos escrever outra equação com base no fato de que o calor perdido pelo líquido B é igual ao calor ganho pelo líquido A (aqui assumimos que não há perdas de calor no sistema e usamos o princípio da conservação da energia):
(80 - Tf ) cB mB = (Tf-40) cA mA
Usando (I):
(80 - Tf ) cB mB = (Tf-40) 3 cB mB
Tf = 50 ºC e portanto alternativa b)
OBS: Perceba que as massas e calores específicos dos líquidos não foram dadas porque seriam canceladas durante os cálculos.
(2000) Em um copo grande, termicamente isolado, contendo água à temperatura ambiente (25ºC), são colocados 2 cubos de gelo a 0ºC. A temperatura da água passa a ser, aproximadamente, de 1ºC. Nas mesmas condições se, em vez de 2, fossem colocados 4 cubos de gelo iguais aos anteriores, ao ser atingido o equilíbrio, haveria no copo:
a) apenas água acima de 0ºC
b) apenas água a 0ºC
c) gelo a 0ºC e água acima de 0ºC
d) gelo e água a 0ºC
e) apenas gelo a 0ºC
Resolução:
Esta questão não requer cálculos, apenas um conhecimento dos conceitos de calor específico e calor latente de fusão.
Inicialmente são inseridos 2 cubos de gelo, e calor é transferido da água para o gelo. O resultado é que a temperatura da água abaixa 24 unidades e todo o gelo derrete. Se 2 cubos mais são inseridos, novamente calor será transferido para o gelo , pois a água encontra-se a 1ºC e portanto numa temperatura mais alta que o gelo. e um pouquinho de gelo se derreterá. Só que desta vez não há calor suficiente na água para derreter completamente estes últimos 2 cubos de gelo, pois isso requer um abaixamento de temperatura de 24 unidades e não de apenas 1. Portanto sobrará gelo e teremos água e gelo em equilibrio térmico.
Resposta: c) gelo a 0ºC e água acima de 0ºC
(2004) Um recipiente de isopor, que é um bom isolante térmico, tem em seu interior água e gelo em equilíbrio térmico. Num dia quente, a passagem de calor por suas paredes pode ser estimada, medindo-se a massa de gelo Q presente no interior do isopor, ao longo de algumas horas, como representado no gráfico. Esses dados permitem estimar a transferência de calor pelo isopor, como sendo, aproximadamente, de :
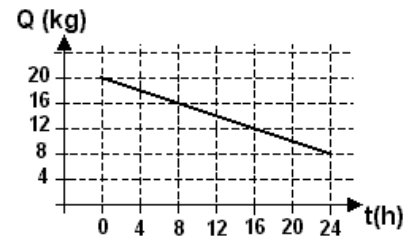
Calor latente de fusão do gelo ≈ 320 kJ/kg
a) 0,5 kJ/h b) 5 kJ/h c) 120 kJ/h d) 160 kJ/h e) 320 kJ/h
Resolução:
Um exercício simples que requer apenas a interpretação do gráfico e a aplicação do conceito de calor latente de fusão.
Segundo o gráfico, houve uma perda de 12 kg de gelo em 24 h. Para que 12 kg de gelo derretam (e a água produzida continue a 0ºC ) a quantidade de calor envolvida é dada pelo calor latente de fusão do gelo multiplicado pela massa:
calor perdido = 12 kg * 320 kJ/kg = 3840 kJ
Esse calor foi perdido durante 24 hs então a taxa de perda é 3840/24 = 160 kJ/h (alternativa d)
Comentário: Foi infeliz a escolha da letra Q para representar a massa de gelo pois Q é normalmente usado para representar calor.
(2009) Um trocador de calor consiste em uma serpentina, pela qual circulam 18 litros de água por minuto. A água entra na serpentina à temperatura ambiente (20ºC) e sai mais quente. Com isso, resfria-se o líquido que passa por uma tubulação principal, na qual a serpentina está enrolada. Em uma fábrica, o líquido a ser resfriado na tubulação principal é também água, a 85 ºC, mantida a uma vazão de 12 litros por minuto. Quando a temperatura de saída da água da serpentina for 40 ºC, será possível estimar que a água da tubulação principal esteja saindo a uma temperatura T de, aproximadamente,
a) 75 ºC b) 65 ºC c) 55 ºC d) 45 ºC e) 35 ºC
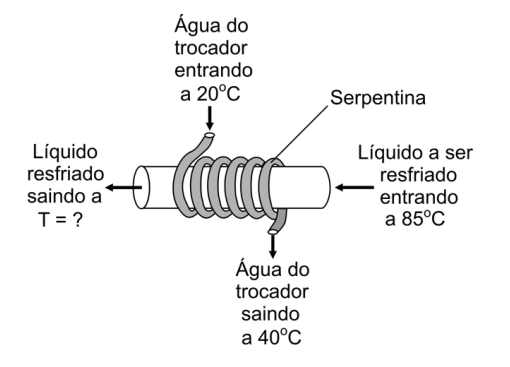
Resolução:
Trata-se aparentemente de um sistema de refrigeração industrial e portanto um cálculo frequente em engenharia química ou mecânica.
Vamos considerar o que acontece neste sistema durante 1 min de funcionamento.
-Parte 1
Chamamos de Q1 ao calor recebido pela água na serpentina (que está sendo usada para refrigerar a água no tubo).
Chamamos de c o calor específico da água e usamos a densidade da água= 1 kg/l .
Esta água é aquecida de 20ºC a 40ºC portanto ΔT=20 :
Q1 = 18 *c *20 = 360 c
-Parte 2
Chamamos de Q2 o calor perdido pela água no tubo:
Esta água é resfriada de 85ºC a Tf e portanto ΔT=85 - Tf:
Q2 = 12 * c * (85 - Tf)
-Parte 3
Equacionando :
A quantidade de calor ganha por um líquido deve ser igual àquela perdida pelo outro e portanto:
Q1 = Q2
360 c = 12 (85 - Tf) c
Eliminando c:
360 = 1020 - 12 Tf
-660 = -12 Tf
Tf = 55 ºC
OBS: Perceba que o calor específico da água não foi dado porque seria cancelado durante os cálculos.
Química e física (calorimetria) nos ataques de 9/11>>
Exercícos sobre calor específico>>
Questões da FUVEST em outros tópicos>>
