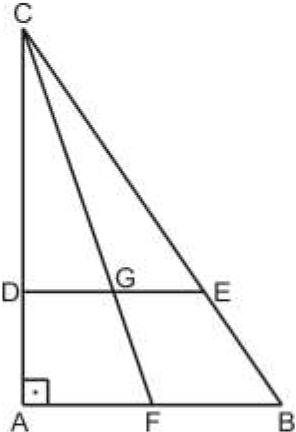
1 ) (FUVEST-2000) Na figura, ABC é um triângulo retângulo de catetos AB = 4 e AC = 5. O segmento DE é paralelo a AB, F é um ponto de AB e o segmento CF intercepta DE no ponto G, com CG = 4 e GF = 2. Assim, a área do triângulo CDE é:

 

Resolução:

Abaixo copio novamente a figura, com as dimensões dos lados (dadas no enunciado):

 

A = CD*DE/2 = 10/3 * 40/15 *1/2 = 400/90 = 40/9

Alternativa : d

---

 

 

2) (FUVEST-2000) Na figura seguinte, estão representados um quadrado de lado 4, uma de suas diagonais e uma semicircunferência de raio 2. Então a área da região hachurada é: 

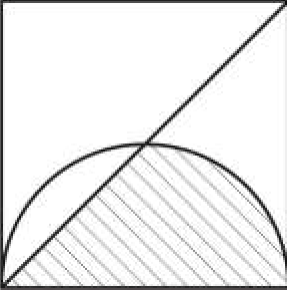
Resolução:

Primeiramente desenhamos um triângulo retângulo (linha vermelha):

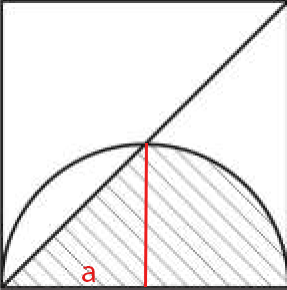
Agora a área da região hachurada é a soma de 1/4 da área do círculo, mais a área do triângulo retângulo:

1/4 da área do círculo = 1/4* π r ² = 1/4*π*4 = π

área do triângulo retângulo = b*h/2 = 2*2/2 = 2

Portanto a resposta é 2+π

Alternativa : b)

---

 

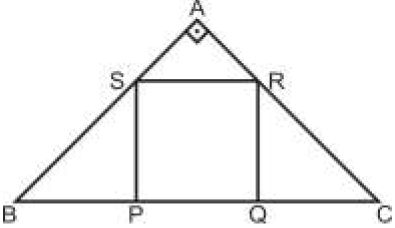
3) Na figura abaixo, ABC é um triangulo isósceles e retângulo em A, e PQRS é um quadrado de lado 2√2 /3.

Portanto, a medida do lado AB é :

 

Resolução:

Os triângulos ASR e ABC são isósceles e retângulos em A. Se traçarmos a altura dos mesmos, dividimos o Ângulo A em 2 ângulos de 45º e cada triângulo se transforma em 2 triângulos, também isósceles. Primeiro analisamos o triângulo ASR:

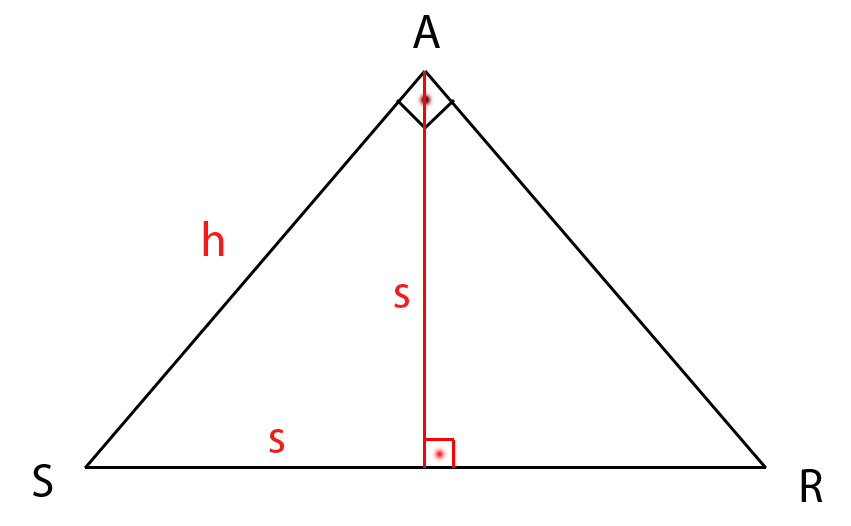
O triângulo construído com catetos vermelhos possui lado s = 2√2 /6

 

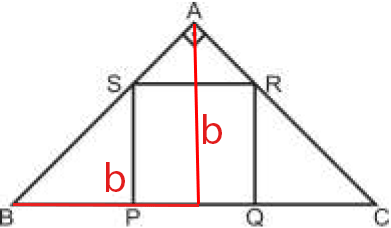
Aqui, o triângulo construído com catetos vermelhos possui lado b = 2√2 /6+2√2 /3=√2 .

 

Para finalmente determinar AB basta usar Pitágoras:

 

(√2)² + (√2)² = AB²

AB = 2

Alternativa: b

---

 

4) (FUVEST-2020) Um objeto é formado por 4 hastes rígidas conectadas em seus extremos por articulações, cujos centros são os vértices de um paralelogramo. As hastes movimentam-se de tal forma que o paralelogramo permanece sempre no mesmo plano. A cada configuração desse objeto, associase θ, a medida do menor ângulo interno do paralelogramo. A área da região delimitada pelo paralelogramo quando θ = 90° é A.

 

 

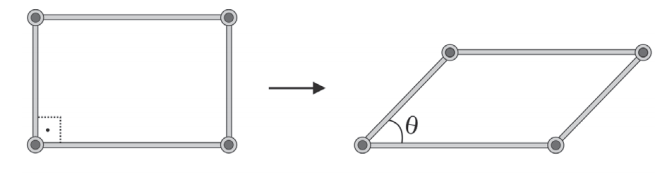
Para que a área da região delimitada pelo paralelogramo seja A/2, o valor de θ é, necessariamente, igual a

a) 15°. b) 22,5°. c) 30°. d) 45°. e) 60°.

 

Resolução:

A área do paralelograma é A = b x h (base vezes altura). Com a movimentação indicada, a altura muda mas a base permanece igual. Portanto para que a área seja reduzida à metade é preciso que a altura seja também reduzida à metade.

Para saber qual o ângulo que corresponde à metade da altura bastante lembrar do ciclo trigonométrico.

 

Resposta: c) 30°

 

Questões da FUVEST em outros tópicos>>