(2007) O isótopo radioativo Cu-64 sofre decaimento Beta ,conforme representado :

 

 

 

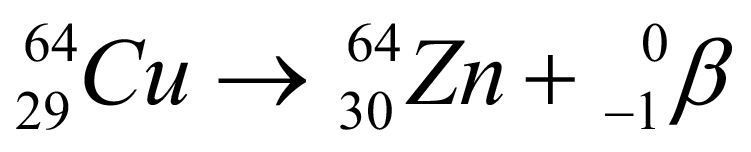
A partir de amostra de 20 mg de Cu-64 ,observa-se que , após 39 horas,formaram -se 17,5 mg de Zn-64. Sendo assim, o tempo necessário para que metade da massa inicial de Cu-64 sofra decaimento é cerca de quanto?

 Resolução:

Perceba-se que não se pode usar regra de três aqui! Esta serve apenas com grandezas que são diretamente proporcionais. São aquelas relacionadas por gráficos com linhas retas.

Lembre-se que a curva do decaimento radioativo é uma exponencial. Nela vemos o decaimento por meias-vidas, ou seja, o número de decaimentos caindo à metade em determinado espaço de tempo. É isso que devemos buscar neste tipo de questão:

 Devido à conservação da massa, os 20 mg de Cu se converterão em 20 mg de Zn. A massa das partículas Beta é desprezível neste caso, quando comparada com as massas dos núcleos.

 Portanto, 2,5mg de Cu restaram depois das 39 horas. Quantas meias-vidas é isso?

 Após 1 meia-vida, restariam 10mg de Cu.

Após 2 meias-vidas, restariam 5 mg de Cu.

Após 3 meias-vidas, restariam 2,5 mg de Cu.

 Assim vemos que passaram-se 3 meias-vidas. Portanto a meia-vida é de 13 horas. Esta é a resposta.

ALTERNATIVA B

 

(2011) O isótopo 14 do carbono emite radiação beta, sendo que 1 g de

carbono de um vegetal vivo apresenta cerca de 900 decaimentos beta por hora valor que permanece constante, pois as plantas absorvem

Continuamente novos átomos de 14C da atmosfera enquanto estão

vivas. Uma ferramenta de madeira, recolhida num sítio arqueológico,

apresentava 225 decaimentos beta por hora por grama de carbono. Assim sendo, essa ferramenta deve datar, aproximadamente, de :

 a) 19 100 a.C.

b) 17 100 a.C.

c) 9 400 a.C.

d) 7 400 a.C.

e) 3 700 a.C.

 Dado: meia vida do C-14: 5700 anos

(PEGADINHA, CUIDADO!)

 RESOLUÇÃO:

 Assim como foi explicado na questão anterior, usaremos o conceito de meia-vida, e calcularemos que após 2 meias-vidas a atividade radioativa cai de 900 para 225:

 900-->450-->225

 Portanto, duas meias-vidas equivale a 2*5700 = 11400

 Demoraria 11400 anos. Mas não tem alternativa?! Atenção à pegadinha: as alternativas referem-se a datas, e não a tempo em anos como calculamos e portanto devemos subtrair esse período de tempo da data atual, para obter a resposta 9400a.C.

 

ALTERNATIVA C)