Matemática > Geometria > Polígonos - Questões de vestibular
<1) Fuvest 2014
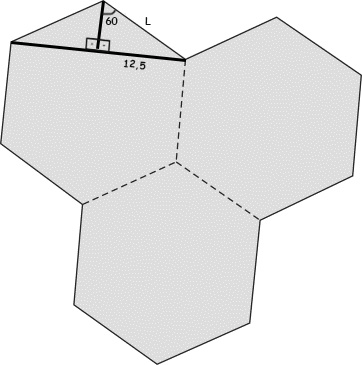
Este problema consiste em calcular a área dos 3 hexágonos regulares, que são iguais. A fórmula calculada para o hexágono regular, na página de áreas, requer o valor do lado. Este valor não é fornecido. Apenas a distância entre lados opostos. Com base na distância entre os lados opostos pode-se calcular o comprimento do lado e depois aplicar a fórmula já conhecida (e facilmente deduzida). Para isso desenhamos 2 triângulos retângulos e usamos a definição do seno:
seno 60 = 12,5 / L
L = 25 √3 / 3
Inserindo-se na fórmula da área do hexágono regular:
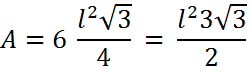
Obtemos :
A = 625 √3 / 2 = 531 (aproximadamente)
Esta é a área de 1 hexágono. Para obter a área total da piscina multiplicamos por 3:
3 x 531 = 1593
Portanto resposta a).
2) Fuvest 2006
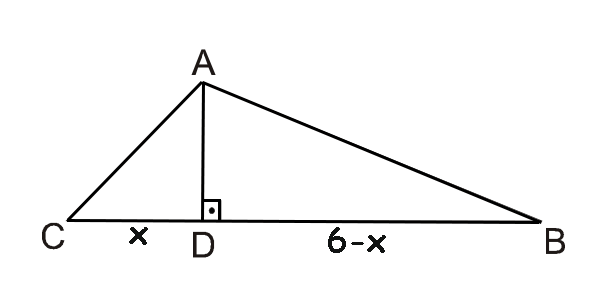
A altura AD é comum aos triângulos ACD e ADB. Portanto a estratégia aplicada aqui será aplicar Pitágoras em ambos triângulos, de modo a escrever 2 equações e descobrir o valor de AD, que chamarei de h.
Chamarei também CD de x e DB de 6-x. Dessa forma:
ADC : h2 = 9 - x2
ADB : h2 = 16 - (6-x)2
9 - x2 = - x2 +12x -20
29 = 12 x
x = 29/12
Alternativa e)
3) Fuvest 2001
Como eu havia dito, triângulos são tão importantes que são usados até em problemas onde não se vê nenhum inicialmente, como este.
Iniciamos desenhando um triângulo que liga os centros dos círculos (que são bases de cilindros):
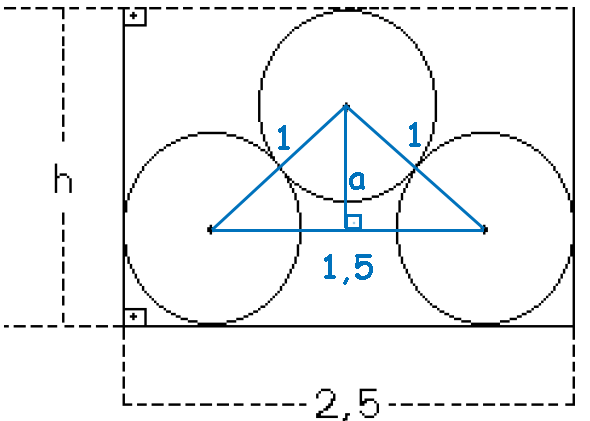
Em seguida traçamos a altura deste triângulo isóceles, de modo que formamos 2 triângulos retângulos. A altura (chamada de a para não confundir com h que é dado no enunciado como a altura do caminhão) pode ser calculada por Pitágoras:
12 = a2 + (0,75)2
Agora um truque: para simplificar a sua conta, use 3/4 ao invés de 0,75!
1 = a2 + 9/16
a2 = 7/16
a = √7 / 4
Agora, para finalizar, somamos o resto das componentes da altura total do caminhão, que seriam um raio r abaixo e outro raio r acima do triângulo desenhado.
Portanto altura total , h, = 1 + √7 / 4
Alternativa e)
4) Fuvest
Este problema é resolvido de maneira análoga ao anterior (3), ou seja, desenhando-se um triângulo que une centros de círculos. Neste caso o triângulo envolverá mais círculos, mas o cálculo será o mesmo..
Alternativa a)