Matemática > Geometria > Polígonos - Parte 3 -Triângulos
Definições e pontos notáveis:
Baricentro- ponto onde se cruzam as medianas
O baricentro divide cada mediana na proporção 2 para 1.
Mediana - linha que vai de um vértice do triângulo até o ponto médio do lado oposto
Bissetriz interna - linha que divide um ângulo em dois ângulos iguais
Incentro- ponto onde as três bissetrizes de um triângulo se cruzam
É o centro da circunferência inscrita no triângulo
Mediatriz - linha perependicular a um lado do triângulo, iniciando-se no seu ponto médio
Circuncentro - ponto onde as 3 mediatrizes se cruzam
É o centro da circunferência circusncrita ao triângulo
Altura - linha que vai desde um vértice até o lado oposto, sendo perpendicular a este (ou à continuação deste, dependendo do caso)
Ortocentro - ponto onde as 3 alturas de um triângulo se cruzam
Perímetro - soma do comprimento de todos os lados
Semiperímetro - metade do perímetro
=========================
triângulo equilátero - tem todos os lados iguais
triângulo isóceles - tem apenas 2 lados iguais
triângulo escaleno - não tem lados iguais (são todos diferentes)
triângulo retângulo - um dos ângulos é reto
Em um triângulo equilátero os 4 centros ( baricentro, incentro, circuncentro e ortocentro) estão no mesmo ponto.
===========================
Semelhança de Triângulos
Triângulos semelhantes possuem todos os ângulos iguais.
O que é mais interessante neles é que seus lados homólogos (aqueles que se correspondem tendo em vista a posição deles com relação aos angulos) são proporcionais. Em consequência disto, outras mediadas tombém serão proporcionais, como alturas, áreas, perímetros, etc.
Esta é uma técnica fundamental para se resolver problemas de geometria plana, incluindo aqueles encontrados em vestibulares.
Existem 3 casos de semelhança de triângulos:
1) Caso AA
AA quer dizer angulo angulo. Se 2 ângulos de um triangulo sao iguais, necessariamente os 3 angulos serao iguais porque a soma deles deve sempres ser 180
2) Caso LAL
LAL quer dizer lado angulo lado. Se tivermos 2 lados proporcionais e os angulos entre eles iguais, nos 2 triangulos, saberemos que os 2 triangulos sao semelhantes.
3) Caso LLL
LLL quer dizer lado lado lado. Se os 3 lados dos triângulos forem proporcionais, teremos triângulos semelhantes.
Exemplo:
Questão FUVEST-2000:
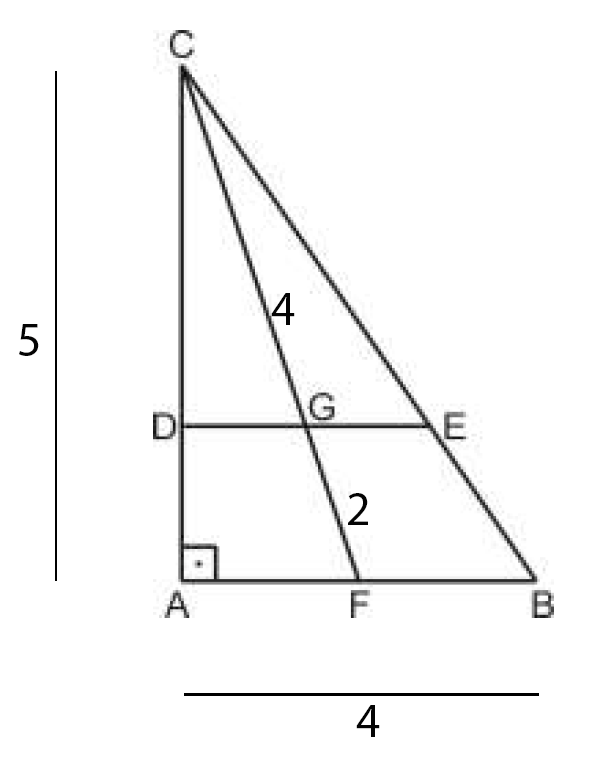
Eu já incluí as medidas que eram dadas no enunciado da questão. Pede-se a área do triângulo CDE.
Para calcular esta área necessitamos saber a base e a altura do triângulo, ou seja, CD e DE.
Exploraremos as relações de semelhança entre 4 triângulos que existem na figura acima.
1) Triângulos CAF e CDG:
CF/CG = CA/CD (lados homólogos proporcionais)
6/4 = 5/CD
20 = 6CD --> CD=20/6 = 10/3
2) Triângulos CAB e CDE
CD/CA = DE/AB (lados homólogos proporcionais)
10/3 * 1/5 = DE/4
10/15 = DE/4
15 DE = 40
DE = 40/15
3) Cálculo da área
A = CD*DE/2 = 10/3 * 40/15 *1/2 = 400/90 = 40/9
-------------------------------------------------------------------------------------
O mesmo principio se aplica também a pirâmides>>
