Physics > Gravity > Newton’s Law of Gravity

Copernicus revolutionised the world with his heliocentric model, where the Earth moves around the Sun. He predicted circular orbits. Kepler, based on lots of observations  found out that the orbits are in fact elliptical and created his 3 laws that describe planetary motion:

Kepler's laws:

1. Planets move in elliptical orbits, with the sun at one focus of the ellipse.

2. A line drawn between the sun and a planet sweeps out equal areas during equal intervals of time.

3. The square of a planet’s orbital period is proportional to the cube of the semimajor-axis length.

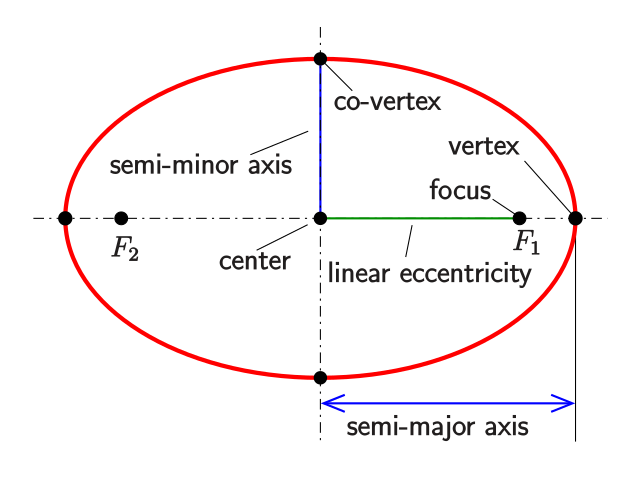
Ellipse and its semi-major- axis. Source: wikipedia - Credit Ag2gae

 

It is interesting to see that all planets obey Kepler´s law, which provide accurate results.

Observe that more equal the axes of the ellipse, the more close to a circle it is. In other words, a circle is a ellipse where the ratio of the length of both axes (major / minor) is 1. This ratio is called eccentricity. The orbit of the Earth has an eccentricity very close to 1 so that is almost circular. We will do orbit calculations only for circles because it is much easier than for ellipses. And that is enough for your IB Physics examinations (standard or higher).

 

Newton’s Law of Gravity

The formula below gives the force of gravity between 2 masses m1 and m2. It depend son the masses and the square of the distance between them. There is also a constant involved: G - the constant of gravity. Its value is: G = 6.67 * 10^-11 N m² kg^-2

$$\begin{aligned} \mathrm{F_{1\to2} = \frac {Gm_1m_2}{r^2}} \end{aligned}$$

The formula refers to the force of 1 on 2 . The force of 2 on 1 is the same. For instance, that Moon pulls the Earth with the same force that the Earth pulls the moon.

This formula is very similar to that used for the electric force, which also depends on the square of the distance and some property of the 2 bodies involved; in this case the property is electric charge instead of mass. The IB formula booklet illustrates it by displaying those equations side by side on section 10.2 - Fields at work. The constant for the electric force is  8.988×10⁹ N m² C⁻². Observe how the units are similar, with C (unit of electrical charge) instead of kg. Observe also that its value is much higher. Because of that, the electric force is much stronger. For the force of gravity to exert a substantial effect , enormous masses are needed, on the order of planets at least.&

Weight and g (acceleration of gravity) - The F=mg formula

For objects on the surface of our planet, the force of gravity is called weight.

You have probably learnt, in more elementary physics courses, that the formula for weight is weight = mg. That comes from Newton's 2nd law of motion : F = ma , where a is the acceleration and in this case it is the acceleration of gravity : g. That is how we get the formula weight = mg (which by the way is not on the IB Physics data booklet).

The acceleration of gravity -g - is also called gravitational field strength.

So, how F = mg relates to the formula for force give by Newton’s Law of Gravity?

The F=mg formula is more simple and it is used for calculations on the surface of the planet and at heights that are not too big (we will see examples in a moment). The value of g at the height of a low orbit (LEO) satellite is very much the same as at the surface. But if you wanted to use the more complicated formula at the surface of the planet , it should give exactly the same result.

In fact, we can equate both formulas to get the value of g, for whatever planet (this calculations are shown on my spreadsheet), but we will look at some examples here.

$$\begin{aligned} \mathrm{m_1g = \frac {Gm_1m_2}{r^2}} \end{aligned}$$

so that

$$\begin{aligned} \mathrm{g = \frac {Gm_2}{r^2}} \end{aligned}$$

where m2 is the mass of the planet.

How does g vary with height?

The height of objects on the surface, or even LEO satellites is very small compared to the Earth´s radius, that is why gravity doesn´t change much. I have another spreadsheet (below) to calculate g at various heights using the formulas below.

To obtain gh, which is at a height h, we add h to the radius of the Earth:

 

$$\begin{aligned} \mathrm{g_h = \frac {Gm_2}{(r+h)^2}} \end{aligned}$$

 

It is better if we get g_h as a function of g so we can rearrange the previous equation:

$$\begin{aligned} \mathrm{g_h = \frac {Gm_2}{r^2(1+h/r)^2}} \end{aligned}$$ so that,

$$\begin{aligned} \mathrm{g_h = \frac {g}{(1+h/r)^2}} \end{aligned}$$

 

 

The spreadsheet shows various calculations of gh. For instance, at a height of 10 km above the surface of the Earth, gh is 9.76, which is hardly any different from gh at the surface (9.79). At the height of a geostationary orbit (35 km) gh is around 9.69, which is not much different either. At the height of the ISS, which is 400 km, gh is 8.67 (that leads to the question which is our next topic). The graph below shows how gh decreases with increased h:

 

 

So, why people are weightless in the Space Station (ISS) if g in there is almost equal to that on the surface of the Earth?

It is because these people are free-falling! They have no floor under the feet, as the whole station is also free-falling. Free-falling means that the only force acting on them is gravity; there is no reaction force from a surface where they stand on. The reason they don´t fall down to the Earth is because they are moving at a very high speed. It is like rotating a stone attached to a string!

It is interesting to notice that to get something on orbit it is not enough to get up in there; a high speed is also needed.

 

Read more: https://sitn.hms.harvard.edu/flash/2018/free-falling-the-science-of-weightlessness/