Revisão ENEM > Matemática > Análise combinatória >> Arranjos (incluindo permutações) e Combinações
Os problemas de análise combinatória involvem cálculos de arranjos e combinações. É essencial saber quando se trata de uma caso ou outro, pois as fórmulas são diferentes (estas serão apresentadas no final desta página). Esse tema é melhor explicado por meio de exemplos.
::Exemplos::
Exemplo de Arranjo: Quantos senhas diferentes podemos formar usando 4 algarismos ?
Resposta: Existem 10 algarismos diferentes. A resposta consiste em calcular arranjos de 10 em 4, representados por A10,4. Usando a calculadora de arranjos abaixo (com n=10 e p =4) obtemos a resposta: 5040 . Perceba que a ordem dos algarismos importa! Quer dizer, a sequencia 1234 é uma senha diferente da sequencia 2134.
--------------Calculadora de Arranjo An,p--------------
n
p
(Para permutação basta fazer n=p)
Exemplo de Combinação: Quantos times de futebol de salão diferentes podemos formar com 10 jogadores?
Resposta: Perceba que a situação é diferente do caso acima com as senhas. No caso de um time de futebol, não interessa a ordem em que são escolhidos os jogadores, pois o time será o mesmo! Ou seja o time João, Pedro, Marcelo, Ricardo e Beto é o mesmo que o time Pedro, João, Ricardo, Marcelo e Beto. Neste tipo de exemplo, calculamos combinações ( e não arranjos). Sacou? Resposta: Combinações de 10 em 5, representadas por C10,5.Usando n=10 e p =5 na calculadora de combinações abaixo obtemos o resultado: 252 .
-------------------Calculadora de Combinação Cn,p-----------------
n p---------Resultado-----------
-----------------------------------------
Mais exemplos de arranjos e combinações:
Exemplo de Combinação: MegaSena. Nesta loteria são sorteados 6 números. Não importa qual a ordem em que saem os números. Quantos combinações diferentes podem ser formadas? Resposta: Combinação de 60 em 6. Confira a seção Combinações, Probabilidades e Mega Sena
Exemplo de Arranjo: Dez pessoas competem em uma maratona. De quantas maneiras elas podem ocupar os três primeiros lugares (no pódio)? Neste caso a ordem dos elementos importa, porque um estará na primeira colocação! Não é o mesmo que estar na terceira. Resposta: Arranjo de 10 em 3.
----------------------------------------------------------
Permutações
Permutações são arranjos onde n e p são iguais.
--------------------------------------------------
Fórmulas
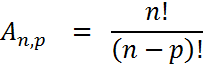
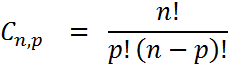
n! , leia-se n fatorial, representa: n(n-1)(n-2)(n-3)...... até o final; consideramos 0! = 1.
Exemplo: Calcular 5!
Resposta: 5*4*3*2*1 = 120
