Química > Básica > Estequiometria

Estequiometria é uma palavra derivada do grego (estequi - elemento; metria-medir). É a parte da química relacionada a cálculos envolvendo quantidades de elementos que reagem e sofrem transformações. Muitas vezes a conta é sobre as quantidades envolvidas, apenas . Outras vezes há relações com outras áreas da química e envolvem também conversão de energia química em calor, luz ou eletricidade.
A boa notícia é que a matemática utilizada é muito simples : tudo pode ser resolvido usando a famosa regra de 3 (como veremos a seguir). A única complicação é que os números utilizados são muito grandes ou muito pequenos, e que uma nova unidade é introduzida: o mole. Ou seja, a estequiometria é o uso de regras de 3 com a unidade mol.

Revisar a regra de 3 >>

O mol

O mol é apenas um número muito grande!
O número é 6,02 * 10²³. Este é chamado de número de Avogadro (cientista italiano do século XIX) . Esta maneira de escrever o número se chama notação científica e significa nesse caso que existem 23 zeros após o número 6. Portanto o número de Avogadro, ou mol, é 602000000000000000000000.
É mais fácil escrever na forma de notação científica né?
Para tentar imaginar o tamanho desse número pensemos em termos de números que conhecemos melhor, como o milhão. Em espanhol, um bilhão costuma ser dito como mil milhões.
Lembremos uma regra matemática: quando se multiplicam potências de mesma base, somam-se os expoentes. Então 103*106 = 109 . Com 10 3 é mil e 10 6 é milhão, temos que um bilhão é igual a mil milhões. Dessa forma o número 10²³ é igual a 10*10³* 10⁹*10⁹ e portanto 10 mil bilhões de bilhões.

Por que um número tão grande? Porque os átomos são muito pequenos. Em 1 g de hidrogênio existe 1 mol de átomos. Um mol é aproximadamente o número de grãos de areia no planeta inteiro.
Se compramos bananas usamos a dúzia, por exemplo. Se falamos de átomos, usamos o mol. Assim como medimos a massa dos nosso corpos em kg mas a massas de caminhões é medida em toneladas.
Embora pareça difícil, a princípio, calcular com esses número enormes, veremos que com o uso da notação científica a conta fica muito simples.

Átomo grama e molécula grama

Mas por que o mol é tão importante? Não poderia ser outro número gigante? Por que este?

Mencionamos acima que em 1g de hidrogênio há 1 mol de átomos. Em 2g de hélio, também há 1 mol de átomos (de hélio nesse caso). Em 3g de lítio, idem. Ou seja, 1 mol de qualquer átomo corresponde à sua massa expressa em gramas ! Dizemos, por exemplo, que 1 átomo grama de H pesa 1 g.

O mesmo se aplica a moléculas. O mapa conceitual abaixo resume essas ideias:

 

 

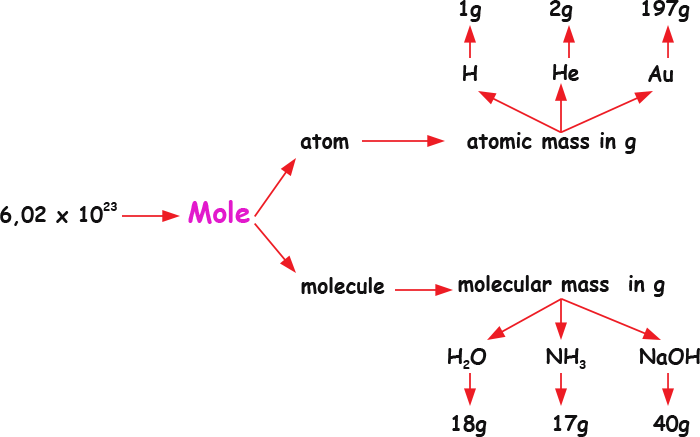
Mapa conceitual : conceitos átomo grama e molécula grama

Estes cálculos são do tipo regra de 3, que você pode revisar aqui.

1- Quantos átomos existem em 10 g de ouro?

Primeiro consultamos a tabela periódica para ver a massa do ouro. Esta é de 196,97 .

Portanto 196,97 gramas de ouro contém 1 mol de átomos de ouro:

massa	número de átomos (mol)
196,97	1
10	x

x = 10 / 196,97 = 0,05 mols

ou 0,05 * 6,02 * 10²³ = 0,3 * 10²³ = 3 * 10²² átomos de ouro

 

2- Quantas toneladas de amônia são produzidas a partir de 1 tonelada de nitrogênio? (suponha que existe hidrogênio em excesso).

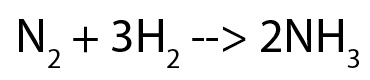
A reação acima nos diz que 1 molécula de nitrogênio reage para formar 2 de amônia.

Como o problema nos informa em gramas, e não em número de moléculas, necessitamos saber a massa das moléculas.

Perceba que aqui usamos o conceito de molécula grama.

A massa da molécula é a soma das massas dos átomos que a compõe:

A massa de uma molécula de N₂ = 2 * 14 = 28

A massa de uma molécula de NH₃ = 14 +3*1 = 17

Como uma molécula de N₂ produz duas de NH₃, temos que 28 g de N₂ produz 34 g de NH₃

 

massa de N2 (g)	massa de NH3 (g)
28	34
1*106	x

x= 34/28 * 10⁶ = 1.3 * 10⁶ g , ou seja, 1,3 ton

 

Agora tente fazer umas questões da FUVEST (não olhe a resposta antes de tentar resolver)