Matemática - Regra de 3 - Um tópico especial - Parte 1 - variáveis diretamente proporcionais

A famosa regra de três e o ENEM

Parte 2 - variáveis inversamente proporcionais

Parte 3 - Regra de 3 composta

Portanto é um ótimo uso do seu tempo aprender ou revisar a regra de 3.

A boa notícia é que é fácil!

A regar de 3 se aplica a variáveis diretamente proporcionais e também para variáveis inversamente proporcionais.

Aqui explicarei on caso das diretamente proporcionais. Na próxima seção estudaremos as inversamente proporcionais e por fim estudaremos a regar de 3 composta.

 

---

A regra de 3 funciona apenas no caso de variáveis diretamente (ou inversamente) proporcionais

Variáveis diretamente proporcionais são aquelas cujo gráfico que as relaciona é uma linha reta, passando pela origem. Ou seja, na função que o define não há nenhum termo elevado ao quadrado ou , cubo ou a qualquer potência maior que um.

Aqui veremos exemplos de física e química, além dos de matemática é claro.

 

Se para fazer um certo bolo são necessários 2 ovos, quantos ovos serão necessários para fazer 3 bolos ?

Nesse caso as variáveis são diretamente proporcionais, porque se o número de bolos a ser feito aumenta, o número de ovos também aumenta.

Tá na cara que a resposta são 6 ovos. Mas a conta seria assim:

Em cada coluna usa-se uma das grandezas consideradas:

bolos	ovos
1	2
3	x

 

Agora escrevem-se 2 frações, de acordo com a tabela:

1/3 = 2/x

em seguida multiplica-se em cruz:

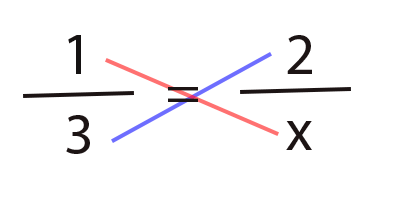
2*3 = 1*x

x = 6/1 = 6

O preço de uma TV é 2 mil reais, mas vai ter 15% de desconto. De quanto será o desconto (em reais)?

Nesse caso também as variáveis são diretamente proporcionais, porque quanto maior a porcentagem do desconto, maior o valor que vai ser descontado (isso parece óbvio mas veremos também exemplos do contrário).

Sabemos que 2000 corresponde a 100% do custo da TV: Como no caso anterior, organizamos os dados em 2 colunas, que nesse caso serão os valores e as porcentagens: Sabemos que 2000 corresponde a 100% do custo da TV:

 

valor	porcentagem
2000	100
x	15

 

Como no caso anterior, multiplicamos em cruz:

2000*15 = 100*x

x= 300

Ou seja, 15% de desconto corresponde a 300 reais.

 

---

Será visto também que cálculos de química são bastante similares a este. Por exemplo, se 3 moléculas de hidrogênio saõ necessárias para se fazer 2 moléculas de amônia, quantas moléculas de hidrogênio são necessárias para se fazer 10 moléculas de amônia? É a mesma coisa não é? Veja a equação:

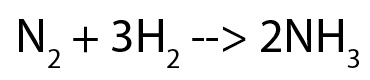
Esta equação representa o processo de Haber, que é extremamente importante para fixar o nitrogênio do ar e poder fabricar fertilizantes, explosivos e mais...

(Resposta: 15 moléculas de hidrogênio).

Fazendo o cálculo explicitamemte temos:

H2	NH3
3	2
x	10

Multiplicando em cruz:

3*10 = 2 x => x = 15

A área dea química que estuda este tipo de cálculo chana-se estequiometria e é uma das que mais caem em vestibulares . Consiste basicamente de uma regra de três que inclui o conceito de mol e às vezes algo mais, relacionado a liberação de energia por exemplo. Mas tudo é diretamente proporcional.

Veja também uma explicação mais detalhada de estequiometria e questões da FUVEST.

Cinemática: velocidade e distância percorrida (física)

Cinemática é o estudo do movimento (-cine: movimento; como em cinema: imagens em movimento). Na verdade são contas simples para quem sabe usar gráficos e regra de 3.

Nesse exemplo temos uma carro viajando à velocidade de 2 m/s. Após 5 s , ele terá viajado 10m. Após 10 s , ele terá viajado 20m. As grandezas são proporcionais e podem ser calculadas por regra de 3. O gráfico abaixo ilustra a situação:

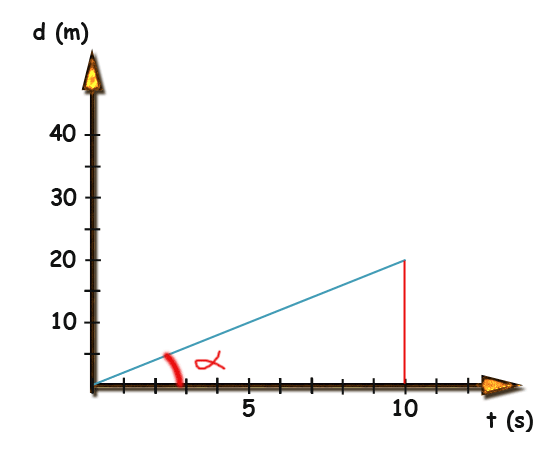
O exemplo acima ilustra que as variáveis diretamente proporcionais podem ser representadas graficamente por linhas retas, o que é bastante útil.