Matemática - Regra de 3 - Um tópico especial - Parte 2 - variáveis inversamente proporcionais
Parte 1 - variáveis diretamente proporcionais
Variáveis inversamente proporcionais podem aparecer em física e matemática, mas não em química. Neste caso deve-se inverter uma das frações, antes de fazer a multiplicação em cruz, conforme explicado no caso anterior (parte 1).
Se uma variável diminui, enquanto a outra aumenta na mesma proporção, diz-se que elas são inversamente proporcionais. O gráfico que relaciona as variáveis neste caso não é taõ simples como no caso anterior, das vatiáveis diretamente proporcionais (linha reta). Neste caso temos a seguinte curva (plotada no google para a função y = 1/x):
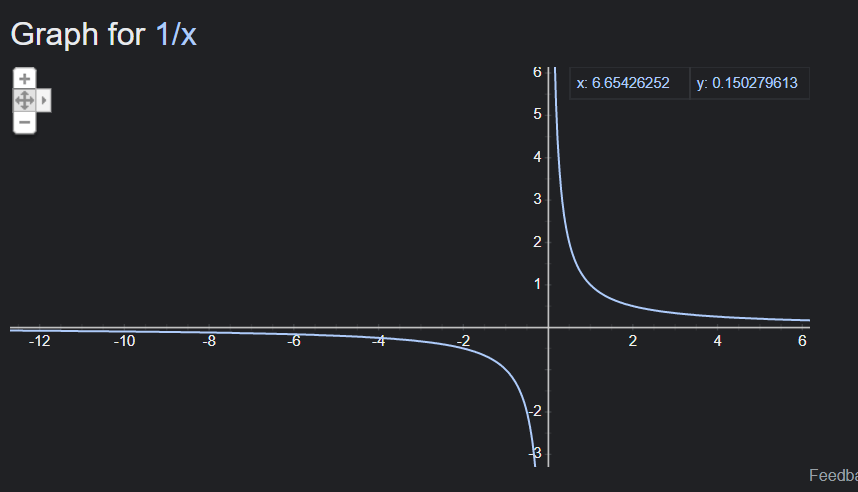
Para y = x (variáveis diretamente proporcionais) temos a linha reta e neste caso em que y é proporcional ao inverso de x, ou seja proporcional a 1/x ,temos esta curva mais complicada.
Exemplo - Matemática:
homens na obra
4 homens terminam uma obra em 2 dias
10 homens terminam em quantos dias?
Resolução: As variáveis homens e dias são inversamente proporcionais, porque quanto mais homens trabalhem, menos dias serão necessários para terminar a obra. O cálculo é semelhante ao caso diretamente proporcional, mas uma das frações é invertida:Normalmente invertemos a fração que não envolve o x.
| homens | dias |
| 4 | 2 |
| 10 | x |
10/4 = 2/x (perceba que a primeira fração -à esquerda- está invertida)
10 x =8 ==> x = 0,8 dia
ou seja, menos de 1 dia.
Exemplo - Física:
A distância de SP ao RJ é 400 km. Se uma viagem de SP ao RJ demora 4hs a uma velocidade de 100km/h, quanto essa mesma viagem demora a uma velocidade de 50 km/h?
Veja que quanto maior a velocidade, menor o tempo de viagem. Portanto as variáveis são inversas.
Montando a tabela:
| v (km/h) | t (h) |
| 100 | 4 |
| 50 | x |
Invertemos a fração que não envolve o x (poderia ser a outra que daria no mesmo):
4/x = 50/100
50*x = 4*100
x = 8 h
Veja que o resultado é inverso e proporcional, porque a velocidade diminuiu pela metade e o tempo dobrou.
Podemos analisar mais esta situação:
Quanto maior a velocidade , menor o tempo de viagem. Se vamos de SP ao RJ são 400km de distância.
A distância (s) , velocidade (v) e tempo (t) são relacionados pela formula:
s = vt
A distância está fixada em 400 km então o tempo t = 400 / v
Tabelando alguns numeros que obedecem esta formula (planilha do excel anexa abaixo):
| v (km/h) | t (h) |
| 50 | 8.00 |
| 100 | 4.00 |
| 150 | 2.67 |
| 200 | 2.00 |
Na tabela acima se vê claramente que conforme a velocidade aumenta o tempo de viagem diminui. Calculando mais valores e plotando o gráfico obtemos: vs v (km_h).png)
A planilha usada nestes cálculos está aqui.
Mais uma vez. é interessante notar que neste caso, de variáveis inversamente proporcionais, a linha é curva. Lembre-se que no caso de variáveis diretamente proporcionais a linha é uma reta.
O gráfico acima é característico da função y = 1/x conforme mostrado acima.
