Química > Radioatividade > Cálculos : meias-vidas e decaimento exponencial

Meia-vida

É o tempo que leva para uma quantidade ser reduzida à metade do valor inicial. Ela é usada em diferentes áreas d a ciência. Por exemplo, em farmacologia a meia-vida biológica é o tempo que leva para metade de uma droga (ou qualquer substância introduzida em um organismo) ser eliminada.

No contexto da radioatividade a meia-vida é o tempo que leva para metade dos átomos em uma amostra decaírem. É importante notar que é um cálculo estatístico e portanto não podemos saber quais átomos irão decair, apenas quantos deles.

Se a meia vida de uma amostra é 1 h, após 1 h restará apenas a metade da atividade radioativa. Depois de 2h, restará 1/4. Depois de 3h, 1/8. E assim por diante, de acordo com a tabela abaixo:

Número de meias vidas passadas	Fração que resta	Porcentagem que resta
0	1⁄1	100.0
1	1⁄2	50.0
2	1⁄4	25.0
3	1⁄8	12.5
4	1⁄16	6.25
5	1⁄32	3.125
6	1⁄64	1.5625
7	1⁄128	0.78125

Tabela adaptada da Wikipédia

---

O radiofármaco citrato de gálio, contendo o radionuclídeo Ga-67, é utilizado em diagnóstico de processos inflamatórios e tumorais. Uma das formas de apresentação do radiofármaco é em ampolas com solução injetável de citrato de gálio. (www.ipen.br. Adaptado.)

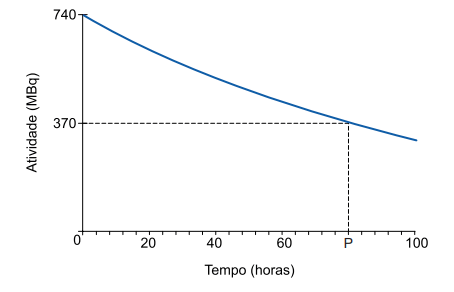
A atividade total da solução na ampola diminui continuamente, a partir da data de calibração (tempo 0), de acordo com o gráfico. Um médico estipulou que, para determinada aplicação desse radiofármaco, a solução da ampola tem que ter atividade mínima de 92,5 MBq. Nesse caso, a ampola só poderá ser utilizada no paciente se for num prazo máximo, a partir da data de calibração, de

a) 13,3 dias. b) 6,7 dias. c) 10,0 dias. d) 16,7 dias. e) 8,0 dias.

Resolução:

A meia vida não é dada explicitamente no enunciado da questão, mas pode ser obtida do gráfico. Ela corresponde à posição P, que é 80 h, que é o tempo para a atividade cair de 740 para 370. Passada outra mia vida a atividade cai para 185 , e passada outra mais cai para 92,5, que é o valor para o qual queremos saber o tempo. Portanto a resposta é 3 meias vidas, ou seja 240 h. Isso corresponde a dez dias, portanto resposta c).

---

 

Para questões mais elaboradas é necessário o cálculo da constante de decaimento, que é o termo a nos gráfico abaixo.

Sistemas que apresentam meias-vidas decaem exponencialmente (função abaixo). Visite meu simulador de função exponencial para sentir como a curva muda de acordo com o valor do expoente (-ax). O simulador permite que selecione valores de a para plotar a curva:

Para podermos calcular a intensidade da radiação em um instante qualquer necessitamos conhecer o termo no expoente (constante de decaimento). Invés de a usaremos a letra grega lambda (λ)  , que é normalmente usada neste contexto. Esta pode ser calculado a partir da meia vida, como mostrarei abaixo. Essa conta exige o conhecimento de logaritmos. Caso não entenda o cálculo, pode-se decorar a fórmula final , que é simples, e é essencial para problemas sobre radioatividade e meias vidas (exceto os mais fáceis).

Chamaremos de N a quantidade de substância. Pode significar número de átomos , massa, ou até mesmo a intensidade da radiação que, no exemplo abaixo , é medida em MBq (megabequerels). N(0) é a quantidade inicial (quando t=0) e N(t) é a quantidade em qualquer instante posterior (a ser calculada), de acordo com a fórmula I:

(I) N(t) = N(0) e^-λt

A equação acima descreve qualquer processo que decai exponencialmente, inclusive o decaimento radioativo.

Chamarei a meia vida de t_1/2. Dessa forma temos que:

N(t_1/2) = N(0) e^{-λ (t 1/2)}

Após t_1/2 , a quantidade N é diminuída da metade:

N(t_1/2) / N(0) = 1/2 = e^{-λ (t 1/2)}

aplicando o logaritmo natural dos dois lados:

ln 1/2 = ln e^{-λ (t 1/2)}

ln 1 - ln 2 = - λ t_1/2

ln2 = λ t_1/2

e finalmente obtemos a fórmula II:

(II) λ = ln 2 / t_1/2

O valor de ln 2 = 0,69 deve ser informado na questão.

Questão da FUVEST sobre o reator nuclear natural (a constante de decaimento é dada) >>

A meia vida do Tc-99m (o isótopo mais usado em medicina nuclear) é de apenas 6 h. Calcule quanto tempo é preciso para que sua atividade radioativa caia a 1 % do valor inicial.

Dado ln 2 = 0,69 e ln 10 = 2,3

Resolução:

A atividade inicial é 100% e a final é 1%.

Usando a fórmula I :

N(t) = N(0) e^-λt

1= 100 e^{-λ t}

Temos ainda duas incógnitas. O λ pode ser calculado a partir da meia vida, usando fórmula II:

λ = ln 2 / t_1/2

λ = 0,69 / 6 = 0,11

Portanto:

1 = 100 e^{-0,11 t}

Sabemos que ln 100 = ln 10² = 2 ln 10 e que ln 1 = 0

-=> aplicando ln dos dois lados da equação:

ln 1 = ln 100 e^{-0,11 t} = ln 100 - 0,11t

0 = 4,6 - 0,11 t

t = 4,6 / 0,11 = 41,8 hs

Veja que após 41,8 hs (menos de 2 dias) a atividade do TC-99m praticamente acaba. Por isso a dificuldade em transportá-lo até os hospitais rapidamente, desde sua produção em um reator de pesquisa ou ciclotron.

No caso do flúor-18, a pressa é ainda maior. Façamos o mesmo cálculo para o flúor-18, que tem meia vida de 110 min.

λ = ln 2 / t_1/2 = 0,69 / 110 = 0,006

1 = 100 e^{-0,006 t}

0 = 4,6 - 0,006 t

t = 766 min = 12,7 h

Devido a essa curtíssimo tempo para o transporte, os hospitais que possuem máquina PET costumam ter também um ciclotron médico pra produzir seus radioisótopos. Outros radioisótopos são também usados, mas todos tem a meia vida curtíssima.

Leia mais em radiofármacos>>

O césio -137 tem meia-vida de aproximadamente 30 anos. Vamos repetir o cálculo anterior. Dessa vez usarei uma planilha do Google para traçar o gráfico.

λ = ln 2 / t_1/2 = 0,69 / 30 = 0,023

0 = 4,6 - 0,023 t

t = 4,6 / 0,023 = 200 anos

Este decaimento é ilustrado no gráfico abaixo. Veja que após 30 anos há uma queda pela metade, como seria esperado.

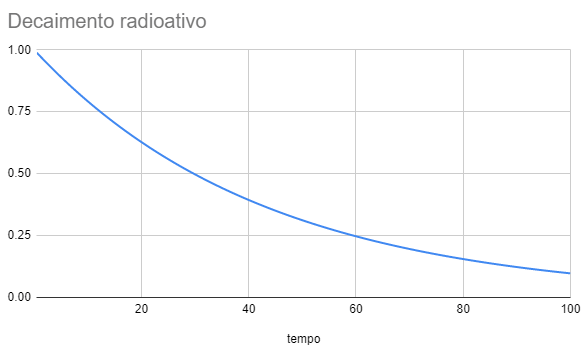
gráfico do decaimento do césio-137

A planilha usada para fazer este gráfico é esta abaixo, que pode ser acessada aqui.

Para fazer mudanças, salve com outro nome no seu Google docs.

 

© Ricardo Esplugas de Oliveira, 2020