Matemática > Geometria > Poliedros - Parte 3 -Octaedro e outros

 

Octaedro

Este poliedro é basicamente constituído de duas pirâmides quadrangulares com suas bases justapostas:

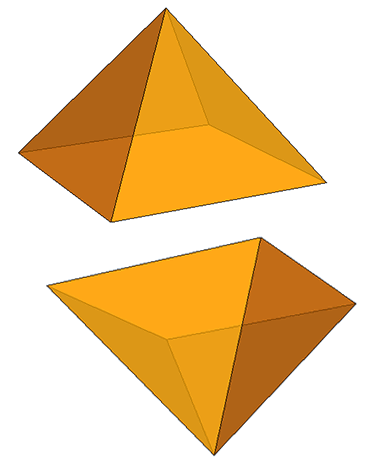
Figura 1 - Duas pirâmides quadradas formando um octaedro

Analisando-se sua planificação percebe-se que é constituído de polígonos iguais e portanto é um poliedro regular:

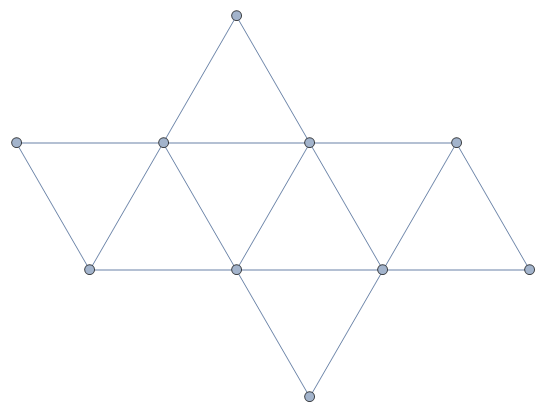
Figura 2 - Planificação do octaedro

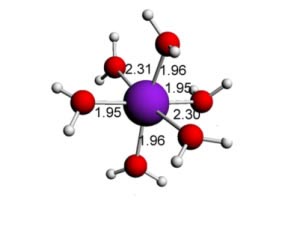
Importantes compostos de coordenação, como esse representado abaixo com suas dimensões, possuem a estrutura octaédrica. a estrutura cristalina da magnetita, pedra importante por ser magnética e também um minério de ferro (óxido de ferro), também é octaédrica. Outro exemplo é a calcita, que é uma forma de carbonato de cálcio. Isso reflete-se na estrutura do mineral como mostrado:

Figura 3 - Estruturas químicas octaédricas

Dodecaedro

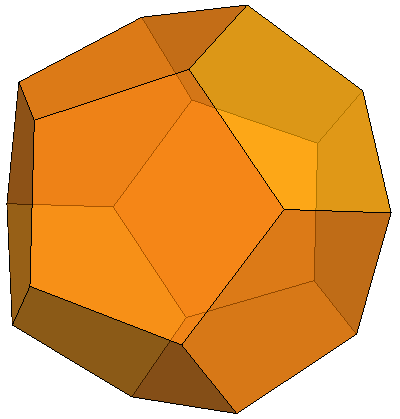
Esse é um poliedro com 12 faces (figura 4). Cada face é um pentágono. Na figura da direita percebe-se que os pentágonos em faces opostas estão em posições invertidas!

Figura 4 - Dodecaedro.

Na planificação do dodecaedro (figura 5) pode-se ver claramente que todas as faces são pentágonos e que existem 12 faces. Analisando-se sua planificação percebe-se que é constituído de polígonos iguais e portanto é um poliedro regular.

 

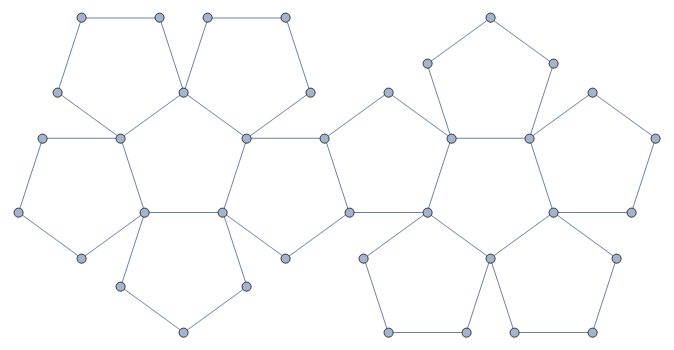
Figura 5 - Dodecaedro planificado mostrando os 12 pentágonos

Icosaedro

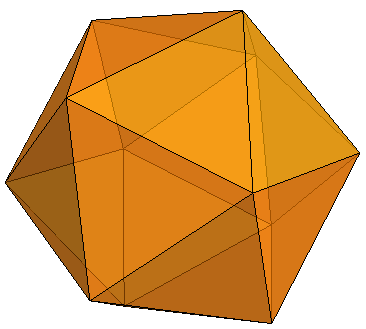
Esse é um poliedro com 20 faces (figura 6). Cada face é um triângulo. Vemos duas imagens do mesmo icosaedro, sendo que a da direita não apresenta transparência.

Figura 6 - Icosaedro

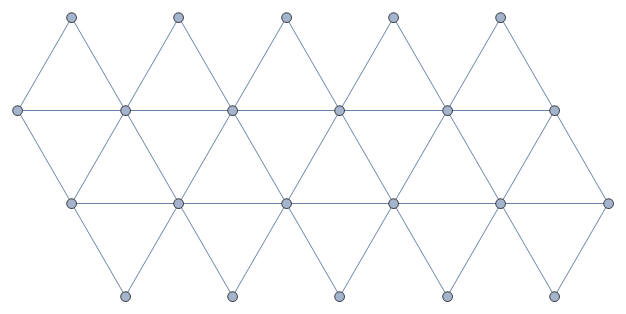
Figura 7 - Icosaedro planificado mostrando os 20 triângulos

Na planificação do icosaedro (figura 7) pode-se ver claramente que todas as faces são triângulos e que existem 20 faces. Analisando-se sua planificação percebe-se que é constituído de polígonos iguais e portanto é um poliedro regular.

---

Para o vestibular já é suficiente. Vou mostrar mais uns poliedros, um pouco mais complicados, apenas por diversão! Chamam-se poliedros estrelados! Imagine se tivesse que fazer cálculos com esses.... (vocês tem sorte!)

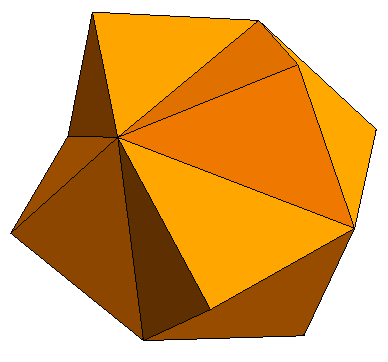
Figura 8 - Octaedro estrelado

Figura 9 - Dodecaedro estrelado

Figura 10 - Icosaedro estrelado

 

 

Parte 4 - Fórmulas, definições e cálculos

Parte 5 - Questões de vestibular

 

 

© Ricardo Esplugas de Oliveira