Matemática > Geometria > Poliedros - Parte 4 - Fórmulas, definições e cálculos
Cálculos de áreas e volumes
Volumes
O mapa abaixo resume as fórmulas de volumes:
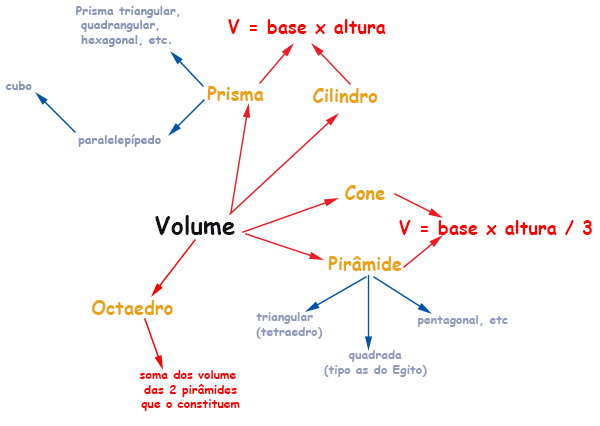
Figura 1 - Mapa conceitual poliedros ver outros mapas>>
Nesse mapa foram incluídos também o cone e o cilindro, devido à suas semelhanças com pirâmides e prismas. Já foi comentado que quando o número de lados do polígono na(s) base(s) aumenta, o poliedro tende a um cilindro (no caso do prisma) ou a um cone (no caso da pirâmide). Na figura do prisma decagonal, em Parte 1, já se nota essa tendência. Imagine com um prisma icosagonal (20 lados)... Portanto, não é surpresa que suas fórmulas para volumes sejam iguais, conforme indicado no mapa acima.
Eu escolhi não incluir uma fórmula para o volume do tronco de pirâmide porque seria mais uma fórmula para decorar.. e uma complicada... Eu acho mais simples calcular esse volume subtraindo o volume da piramide que foi removida do volume total da pirâmide ( tronco = volume total menos volume removido). Esse cálculo será mostrado abaixo.
Áreas
O cálculo de áreas de poliedros não necessita nenhuma fórmula nova: basta calcular as áreas de todas as faces e somar. Isto é feito usando as fórmulas de área dos polígonos.
Exemplo 1 - Qual a área do cubo com arestas de medida 5 cm? Trata-se de um poliedro regular, com 6 faces. Cada face é um quadrado e portanto a área é 52 =25cm. Temos 6 faces portanto Acubo = 6 * 25 = 150 cm2
Exemplo 2 - Qual a área do octaedro com arestas de medida 5 cm? Trata-se de um poliedro regular, com 8 faces. Conforme visto em parte 3, o octaedro consiste de 8 triângulos. Basta calcular a área de cada triângulo e multiplicar por 8.
Fórmula relacionando número de arestas, vértices e faces - Teorema de Euler
Para todo poliedro convexo vale a relação:
V-A+F=2
Essa fórmula deve ser memorizada porque encontra-se questões do tipo:
(PUC-SP) Qual é o poliedro que tem 12 vértices e 30 arestas?
Resposta: 12-30=F+2 --> F = 20 --> icosaedro
Poliedros de Platão
Classificamos como poliedro de Platão aquele que obedece a relação acima (Teorema de Euler) e, além disso, apresenta o mesmo número de arestas em cada face e em cada vértice.
Exemplos: Uma pirâmide quadrangular não é um poliedro de Platão porque a base -que é um quadrado - possui 4 arestas enquanto os lados -que são triângulos-possuem 3 arestas . Um tetraedro é um poliedro de Platão, assim como um cubo também é um poliedro de Platão.
Existem 5 poliedros de platão: Tetraedro, Octaedro, Icosaedro, Hexaedro e Dodecaedro
Poliedros Regulares
São aqueles em que todas as faces são o mesmo polígono regular. São eles:
Tetraedro
Hexaedro (cubo)
Octaedro
Dodecaedro
Icosaedro
Eles podem ser lembrados pela sigla THODI .
Soma dos ângulos
A soma dos ângulos de todas as faces do poliedro convexo é dada por:
S = (V-2)*360
Diagonal do prisma
Esta é calculada da mesma maneira que a diagonal do quadrado ou retângulo: usando o teorema de Pitágoras. A diferença é que agora o cálculo envolve 3 dimensões, mas é basicamente a mesma coisa.
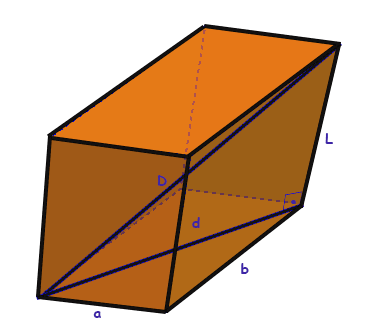
Analisemos a figura abaixo:
 sss
sss
Podemos calcular a diagonal do retângulo (face inferior) usando: a2+b2=d2
Em seguida usa-se Pitágoras novamente em três dimensões:
d2+L2=D2, e encontra-se a diagonal do cubo (D).
Nada de novo, mas requer um pouco de inteligência espacial. Para quem achou complicado relaxe porque ao fazer mais exercícios já se vai acostumando... Mais uma vez, não recomendo decorar fórmula para esse cálculo, é melhor fazer isso na hora da questão, afinal é apenas aplicar Pitágoras (existem livros que oferecem fórmulas prontas para a diagonal do paralelepípedo e outros prismas)...
Semelhança de pirâmides
Assim como temos as propriedades de semelhança de triângulos, que nos ajudam a resolver muitos exercícios e problemas, temos também a semelhança de pirâmides! Não é grande surpresa que estas existam porque afinal as pirâmides são feitas de triângulos (todos os lados são triângulos). Esta relação é particularmente útil para calcular volumes de troncos de pirâmides. Estudaremos as pirâmides abaixo, sendo uma com base de área A2, altura H2 e aresta de base L2 e outra com base de área A1, altura H1 e aresta de base L1.
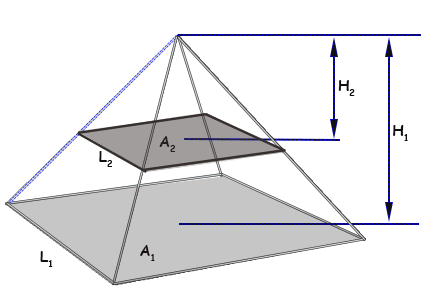
A razão de semelhança será representada pela letra R:
H1 / H2 = L1 / L2 = R
Temos também relações para as áreas e o volume:
A1 / A2 = R2
V1 / V2 = R3
Exemplo de cálculo:
(UNESP-SP) – A figura abaixo representa uma pirâmide
com vértice num ponto E. A base é um retângulo ABCD e a face
EAB é um triângulo retângulo com o ângulo reto no vértice A.
A pirâmide apresenta-se cortada por um plano paralelo à base,
na altura H. Esse plano divide a pirâmide em dois sólidos: uma
pirâmide EA’B’C’D’ e um tronco de pirâmide de altura H.
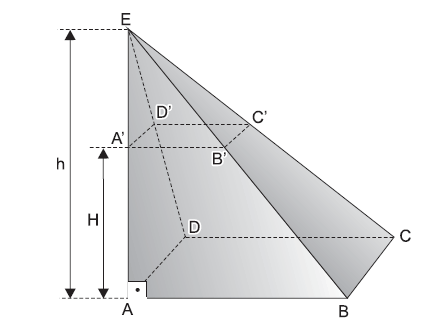
Sabendo-se que H = 4 cm, AB = 6 cm, BC = 3 cm e a altura
h = AE = 6 cm, determine:
a) o volume da pirâmide EA’B’C’D’;
b) o volume do tronco de pirâmide.
Resposta:
É um exercício fácil porque basta aplicar a fórmula diretamente, como mostrarei aqui. O problema maior ao meu ver é que a figura está mal feita pois os valores para altura estão desenhados de modo que parecem ser medidas da face frontal da pirâmide. Mas como sabemos que são alturas vamos lá:
a) Já sabemos a altura desta que é 6-4 = 2. para calcular seu volume precisamos também da área da base. O comprimento das aresta podem ser obtido pela relação de semelhança:
6/2 = 6/A'B' --> A'B' =2
6/2 = 3/B'C' --> B'C' = 1
Volumepequena = 2 *1 *2/ 3 = 4/3 cm
b) Este pode ser obtido subtraindo o volume da pequena pirâmide calculado acima do volume da pirâmide inteira (Vinteira):
Vinteira = Ainteira h
Ainteira = 18
Vinteira = 18*6 / 3 = 36
Vtronco = Vinteira - Vpequena
Vtronco = 36 - 4/3 = 104/3 cm
Parte 5 - Questões de vestibular
© Ricardo Esplugas de Oliveira
