Matemática > Geometria > Poliedros - Parte 1 -Prismas
Poliedros são figuras geométricas tridimensionais que possuem faces planas e que delimitam um espaço finito.

Estrelas (de Esher)
A beleza dos poliedros não é apenas uma criação da matemática mas é uma propriedade da natureza, como será mostrado aqui, usando exemplos de arte e ciência, incluindo víru, proteínas s e até protozoários (radilolaria), pedras semi-preciosas e outros cristais cujas geometrias internas possuem formas poliédricas variadas. Dessa forma pode-se aprender química, geografia, biologia e matemática de uma maneira única e mais interessante. Os poliedros são também muito usados na arte, como por exemplo no trabalho de Leonardo da Vinci e Escher.
Essa abordagem interdisciplinar visa despertar o interesse e motivação e também aumentar a retenção dos temas na memória do estudante. Os cálculos e fórmulas são deixados para uma seção posterior, de modo que o aluno possa apreciar a beleza do tema antes de entrar nos detalhes técnicos, os quais também têm sua beleza mas esta é apreciada por menos pessoas, infelizmente.
Quando falo em poliedros nesta seção refiro-me sempre a poliedros convexos. Estes são os únicos tratados aqui e também os que interessam para os seus exames. Um poliedro é basicamente uma figura geométrica com várias faces, as quais são polígonos. Esta figura ocupa uma porção definida de espaço, a qual chamamos de volume. Outra grandeza de interesse será a sua área total (soma das áreas de todas as faces). Vamos começar com um exemplo, o prisma:
PRISMA
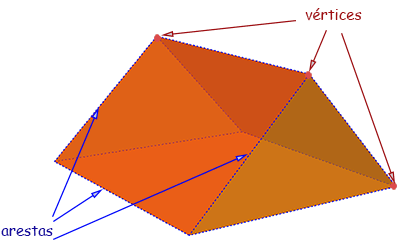
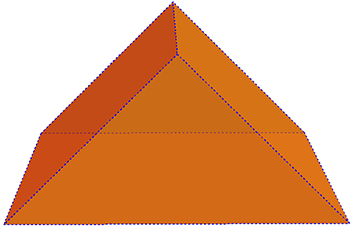
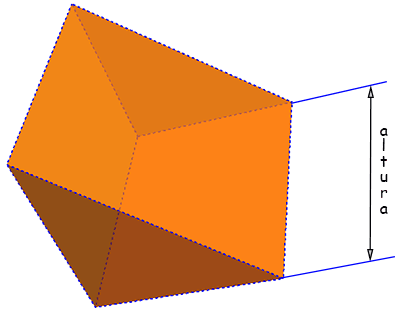
Figura 1 - Prisma triangular visto desde 3 ângulos diferentes
A figura acima mostra que as arestas (linhas pontilhadas em azul) delimitam os lados dos polígonos, que por sua vez constituem as faces do prisma. Os vértices são os pontos onde as arestas se encontram e são também os vértices dos polígonos . Estes conceitos de aresta, vértice e face aplicam-se a todos os poliedros (e não somente ao prisma acima).
O prisma é caracterizado pela presença de dois polígonos situados em planos paralelos (essas 2 faces chamam-se bases) unidos por linhas paralelas (arestas). A distância entre as duas bases chama-se a altura do prisma. No caso do prisma acima as arestas são perpendiculares às bases, e por isso trata-se de prisma reto (possui ângulo reto); se esse não fosse o caso o prisma seria oblíquo. No caso acima as bases são triângulos e portanto o prisma é classificado como prisma triangular. Invés de triângulo, a base poderia ser qualquer polígono. Poderia ser hexágono ou decágono, por exemplo (figura 2):
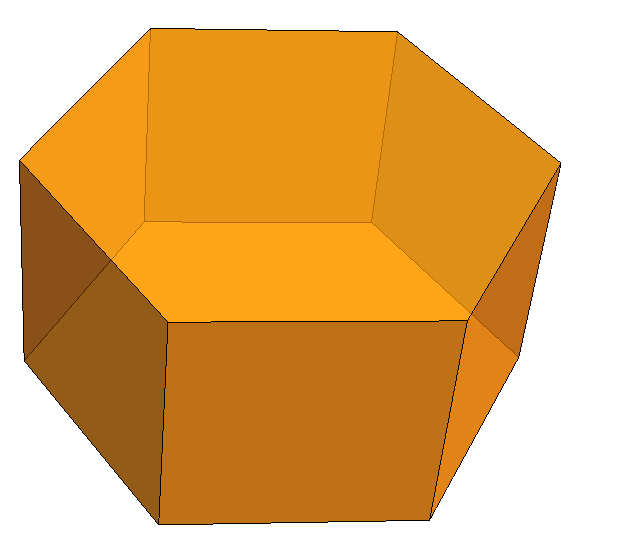
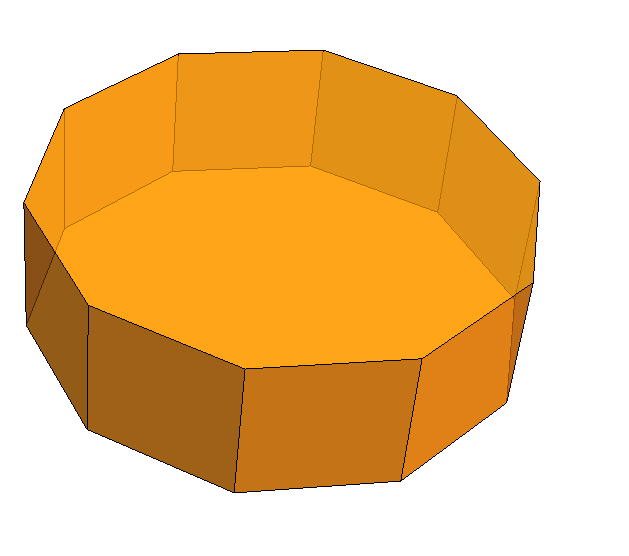
Figura 2 - Prismas hexagonal (esquerda) e decagonal (direita)
Como exemplos na natureza, observamos que diversas estruturas cristalinas apresentam a forma de prisma. Por exemplo a turmalina, pedra semi-preciosa, possui uma estrutura de prisma hexagonal (figura 2). 
Figura 3 - Turmalina "watermellon" exibindo geometria prismática hexagonal (© R. Esplugas)

Figura 4 - Berilo - prisma hexagonal
Outro exemplo natural de prisma hexagonal é o berilo (figura 4).
Perceba que podemos fazer o prisma com polígonos de base de qualquer número de lados, apesar que o máximo que usamos aqui foi 10 lados (prosma decagonal). Quanto maior o número de lados do polígono de base, mais o prisma se aproxima do cilindro.
Existem outros poliedros que nos são familiares e que também são prismas, embora tenham outros nomes mais específicos, como o cubo e o paralelepípedo.
Paralelepípedo
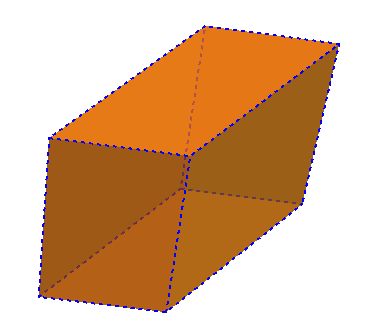
Figura 5 - Paralelepípedo
Este termo é geralmente usado para referir-se à pavimentação de certas ruas, que é feita com pedras que tem esta forma. Paralelepípedo é um prisma cujas bases são paralelogramos.
No caso em que todas as arestas são iguais, e portanto cada face é um quadrado, passamos a ter um cubo. O cubo também é conhecido como hexaedro, porque possui 6 faces.
Como no caso do prisma, temos um paralelepípedo reto se os ângulos entre a base e as arestas for reto.
A geometria interna dos cristais de fluorita possui a forma cúbica. Os átomos de flúor (em cor azul) e de cálcio (verde) estão arranjados na maneira mostrada na figura 4.
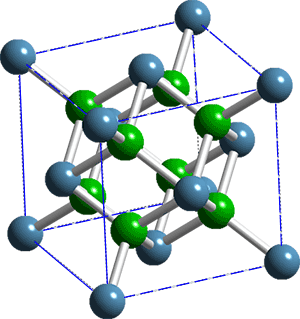
Figura 6 - Fluorita - estrutura (© R. Esplugas)
Ainda mais interessante é o fato de que esta estrutura íntima e profunda do cristal reflete-se na sua aparência macroscópica, isto é, quando olhamos para o material podemos visualizar os cubos (figura 5). Isso acontece porque o cristal cresce sempre de acordo com a sua estrutura, pois este arranjo de átomos confere a menor energia e portanto é a configuração mais estável ( a energia depende basicamente de repulsões e atrações eletrostáticas entre os átomos). Outros poliedros mais complexos também são observados macroscopicamente em cristais, como veremos mais adiante. Uma das mais recentes descobertas feitas baseadas na ciência dos poliedros foi a do fulereno, com 60 átomos de carbono. Será estudado em detalhe.

Figura 7- Fluorita e seus cristais cúbicos (© R. Esplugas)
Parte 2 - Pirâmides incluindo o tetraedro
Parte 3 - Octaedro, dodecaedro, icosaedro
Parte 4 - Fórmulas, definições e cálculos
Parte 5 - Questões de vestibular
© Ricardo Esplugas de Oliveira
